DeveLife

Contents

[course] 모두를 위한 딥러닝 강좌 05

2020/01/20

이 포스팅은 인프런 머신러닝 강좌 를 수강하며 공부한 내용을 정리한 것입니다.
코드 출처

Lecture 5. Logistic Classification

Logistic classification은 classification algorithm들 중에서 정확도가 높은 것으로 알려져 있다.
때문에 실제 문제에도 바로 적용해볼 수 있고, Neural Network와 Deep learning을 이해하는 데 중요한 컴포넌트이다.

recap

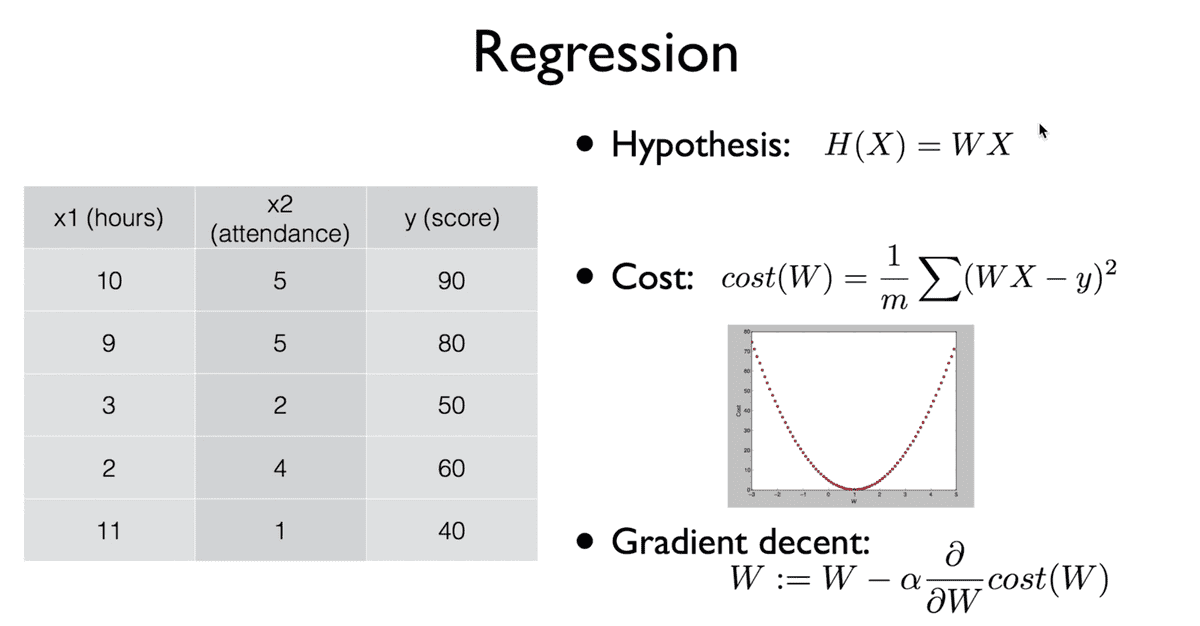
Logistic Classification에 대해 이야기를 도입하기 앞서, 지난 시간까지의 Linear Regression에 대한 정리를 하고 넘어가자.

  1. 우선 가장 먼저 가설을 세운다. 가설은 변수 x에 대하여 선형적이며 우리가 가진 데이터가 어떠한 방식으로 나타날지를 가정하는 일차 함수이다.
  2. 비용 함수를 정의한다. 비용 함수는 학습 목표인 W에 대한 함수이며 가정한 값과 참값 y값의 차의 제곱을 평균을 취한 것이다.
  3. 이 비용 함수는 그림으로 그려보면 밥그릇을 뒤집은 모양으로 나타남을 알 수 있는데, 이러한 그래프를 띠는 함수를 Convex function이라고 한다.
  4. 그리고 이러한 비용 함수에 대하여 결국 비용이 가장 작은 값을 갖게 되는 W 값을 찾는 것이 목적인데, 이를 찾는 알고리즘이 경사를 내려간다는 의미의 Gradient descent알고리즘이다.
  5. 이 알고리즘은 현재의 W깂에서 그 점에서의 기울기를 뺀 값으로 나타나고, 이를 반복 적용함으로서 결과를 도출한다. 기울기는 Cost function을 미분한 값이며 alpha 값은 learning rate라고 불리는 작은 상수 값이다.

Classification

Linear Regression은 어떠한 숫자를 예측하는 것이었다면, 오늘 다룰 Classification은 Binary의 개념 (둘 중 하나를 고르는) 이라고 할 수 있다. 예를 들면 이러한 것이다.

  • 스팸 메일인지 아닌지를 탐지하는 것
  • Facebook에서 News feed 선별 알고리즘
  • 신용 카드 학습 패턴 분류를 통한 도난 여부 식별
  • 두뇌 이미지 분석을 통해 종양 악성 여부 판별
  • 주식 시장 동향 분석을 통해 매입,매도 여부 판별

pass(1)/fail(0) based on study hours

아래와 같은 그림과 함께 생각해보자. 어떤 학생이 공부한 시간에 따라서 시험에 합격과 불합격을 분류하도록 학습 모델을 만들려고 할 때, 직관적으로 생각하면 그냥 Linear regression으로도 가능할 것이라는 생각이 들 수 있다.

recap

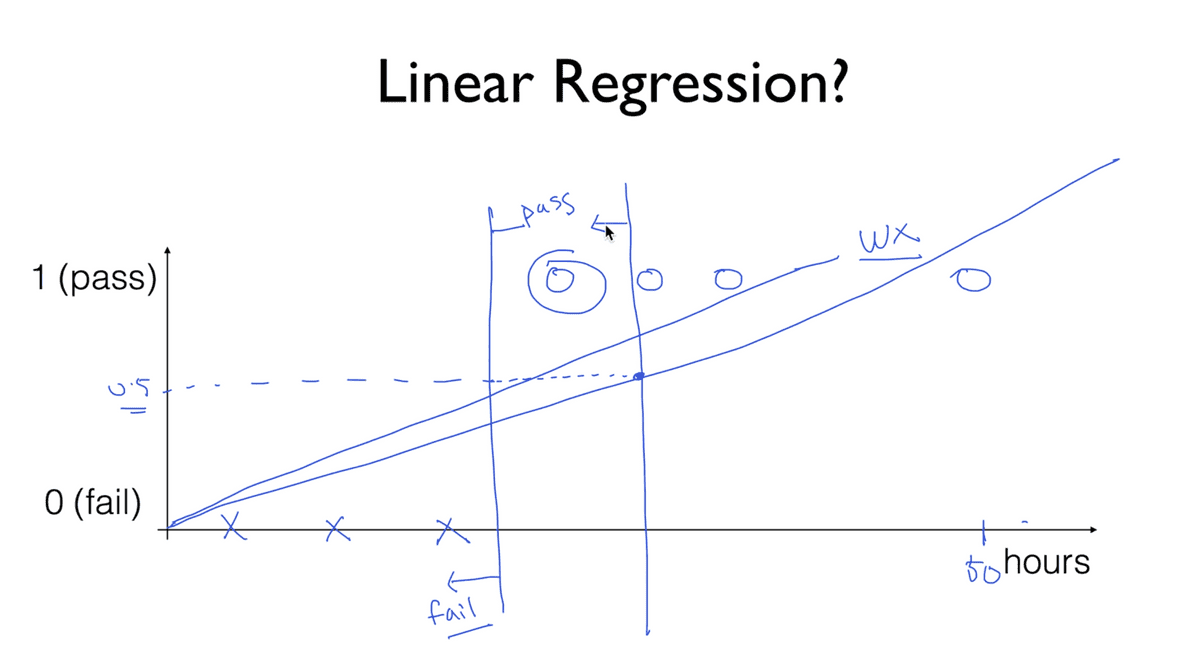
그러나 여기에는 몇 가지 오류가 존재한다. 기존에 3개의 합격, 3개의 불합격 데이터를 가지고 합,불 여부를 결정짓는 어떤 지점을 찾았다고 가정하면 만약에 50시간을 공부해 합격한 학생이 있다고 했을 때, 이 모델은 결국 모든 데이터를 아울러 선형적으로 결정되기 때문에 그 값이 변할 수 있고, 결국 원래 합격이라고 판단되어야 할 학생이 불합격 기준으로 넘어갈 수밖에 없는 상황이 발생한다.

또 다른 문제는, Classification에서는 반드시 값이 0 또는 1로 결정되어야 하는데, Linear regression에서의 Hypothesis는 0보다 훨씬 작거나 1보다 훨씬 큰 값이 나올 수가 있게 된다.

Logistic Hypothesis

따라서 Logistic Classification에는 값의 범위를 0과 1로 제한하는 함수가 필요하다. 많은 이들의 연구 끝에 다음과 같은 함수가 이 모델에 가장 적합한 모습으로 채택되었다고 한다. 기존에 알고 있던 WX를 z로, H(x)를 g(z)로 변환하여 Logistic의 가설 함수를 표현한다.

sigmoid

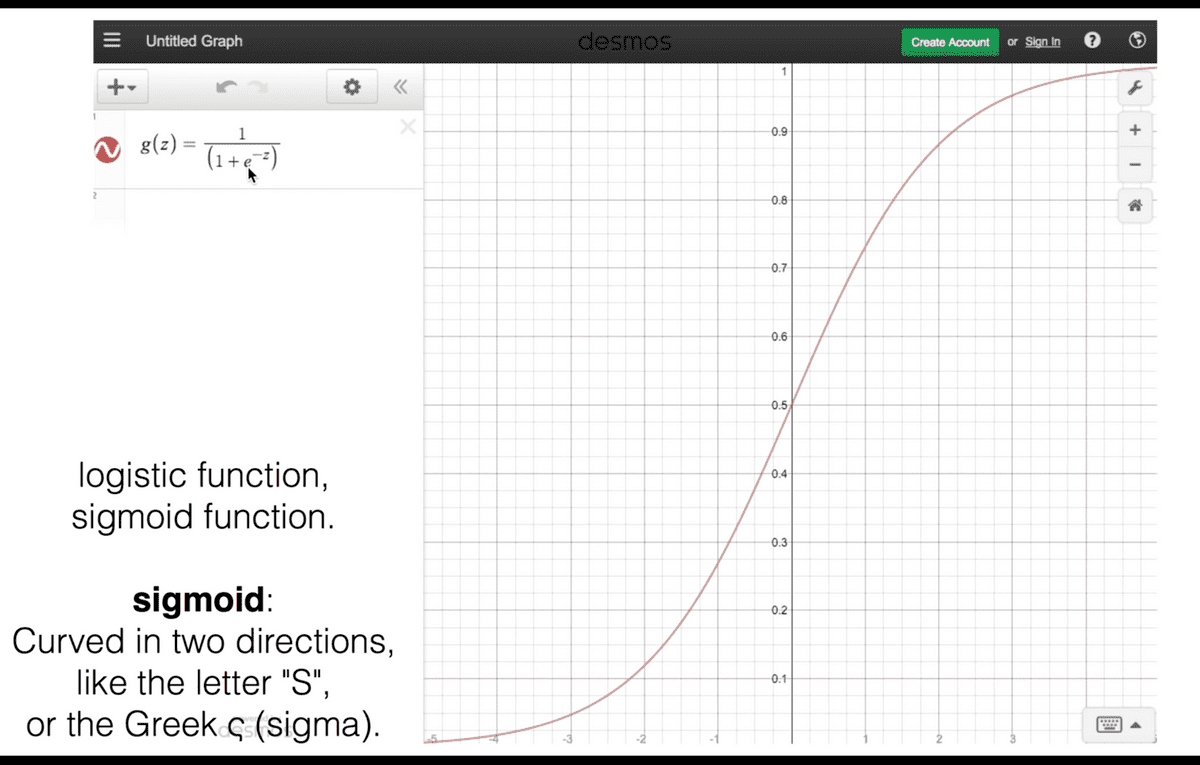
이와 같은 함수를 Logistic function, 혹은 Sigmoid function 이라고 부른다. 가로 축 z값이 무한히 커질수록 g(z) 값은 1에 수렴하게 되고, z가 무한히 작아지면 0에 수렴하게 된다.

sigmoid

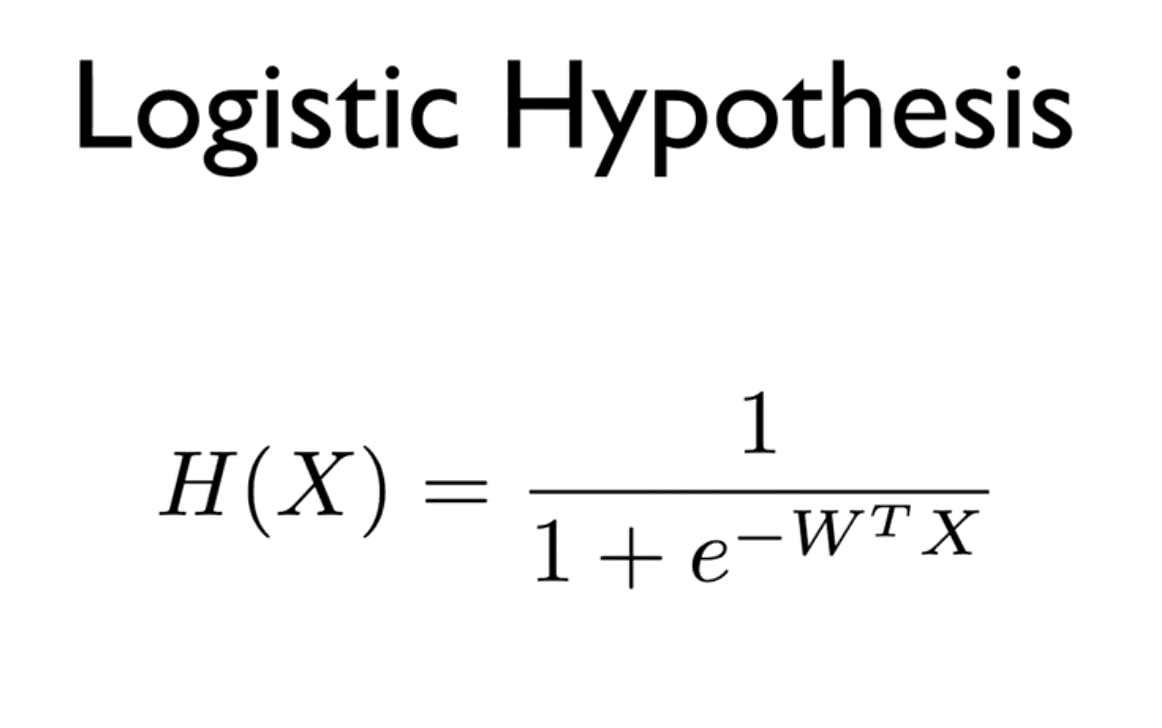
정리하면 Logistic Classification의 가설 함수는 위와 같이 형태가 된다.


5-2 Cost function & Gradient descent in Logistic classification


cost function

sigmoid

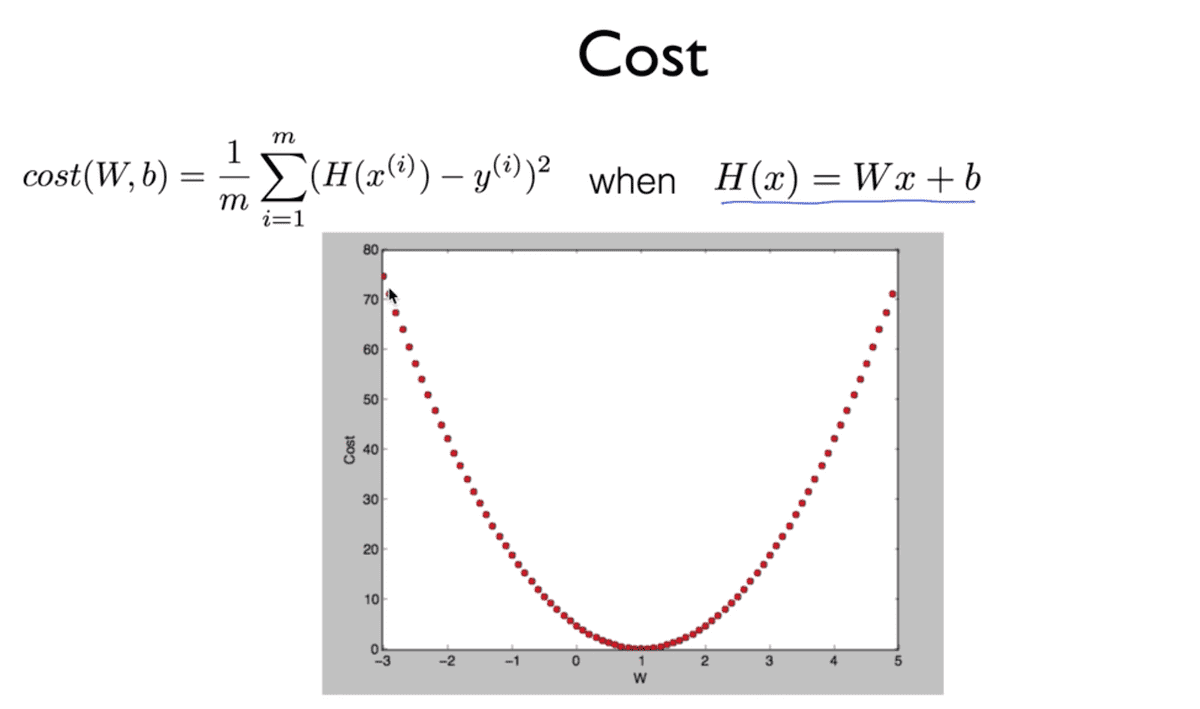
기존의 우리의 Cost function은 위와 같은 형태를 띠고 있었다. 이러한 형태의 함수가 가지는 장점은 어느 지점에서 시작하더라도 Cost가 최소가 되는 지점을 반드시 찾을 수 있다는 것이었다.

cost

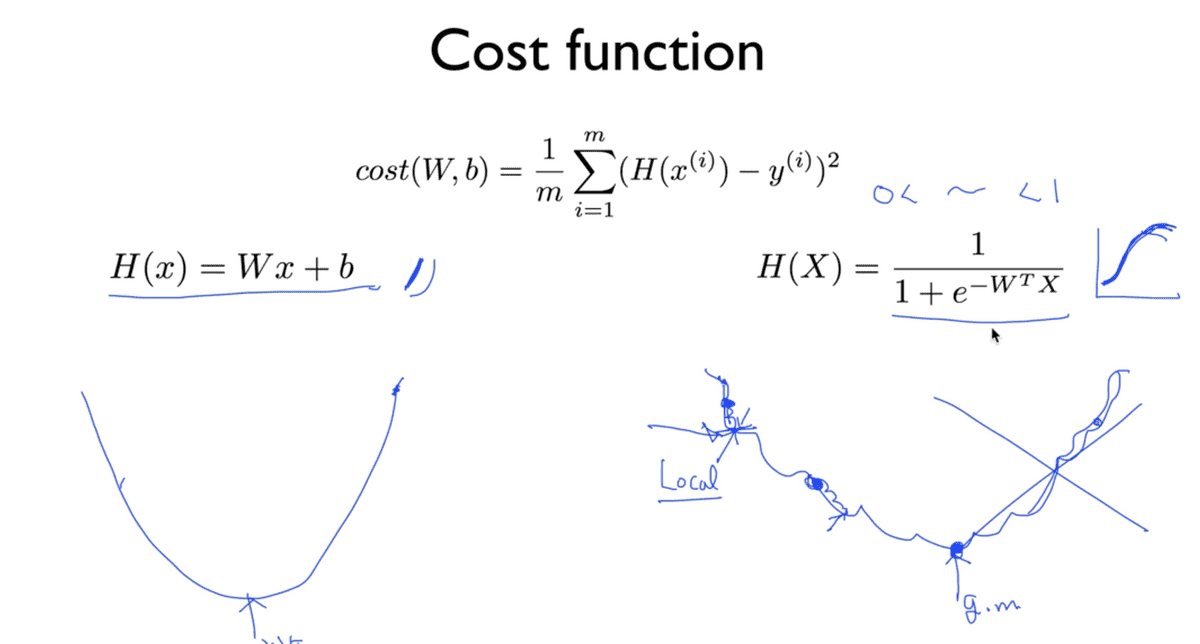
기존의 Hypothesis를 바탕으로 한 Cost function에서는 이차 방정식의 그래프의 형태를 가지기 때문에 어느 지점에서 시작하든 cost가 최소가 되는 지점을 찾을 수 있었던 데 반해,

Sigmoid function을 가설 함수로 갖는 Logistic classification에 동일한 Cost function을 적용하게 되면 그림 우측 하단과 같이 구불구불한 형태를 가지게 된다. 이로 인해서 시작하는 지점에 따라서 함수 전체의 최소 값(global minimum)을 찾을 수 없게 되고, Local Minimum이라는 특정 부분의 최소 지점에서 멈춰버리게 된다. 따라서 Linear에서와 다르게 변화된 Hypothesis에 맞추어 cost function 또한 다르게 적용해야 모델이 올바르게 예측할 수 있도록 할 수 있다.

cost

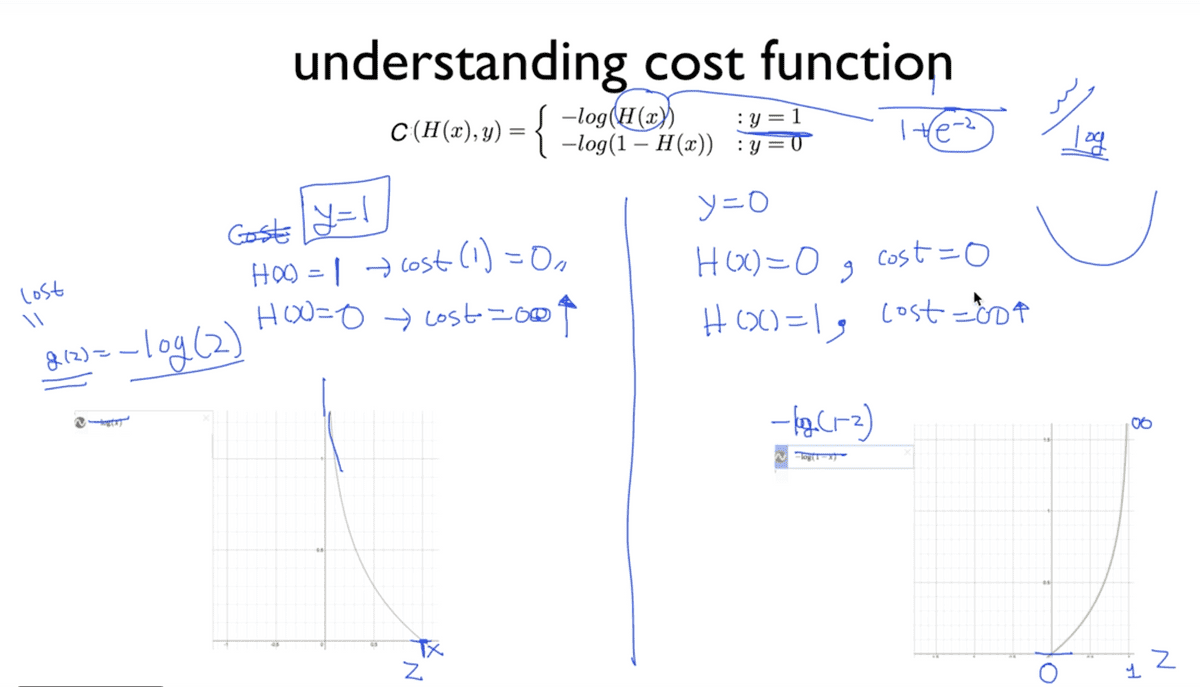
Logistic Classification의 Cost function은 사진의 제목 아래에 보이는 것과 같이 y의 값이 0일 때와 1일 때로 나누어서 살펴볼 수 있다. 앞서 우리가 세운 새로운 가설 함수에 e 즉, exponential이 포함되어 있어 그래프가 구불구불해지는 현상 때문에 그와 상극인 log를 취해주어 부드러운 곡선의 형태로 만들어주게 된다. 그리고 이 정의에서 0과 1로 나눈 중요한 포인트는 각 경우마다 예측이 성공했을 경우 0의 값을 갖고, 틀렸을 경우 무한대로 수렴하도록 하는 로직이 포함되어 있기 때문이다. 이를 c function이라고 이름 짓고, 이들의 합을 구해 평균을 취한 것이 우리가 찾고자 하는 cost function이 된다.

cost

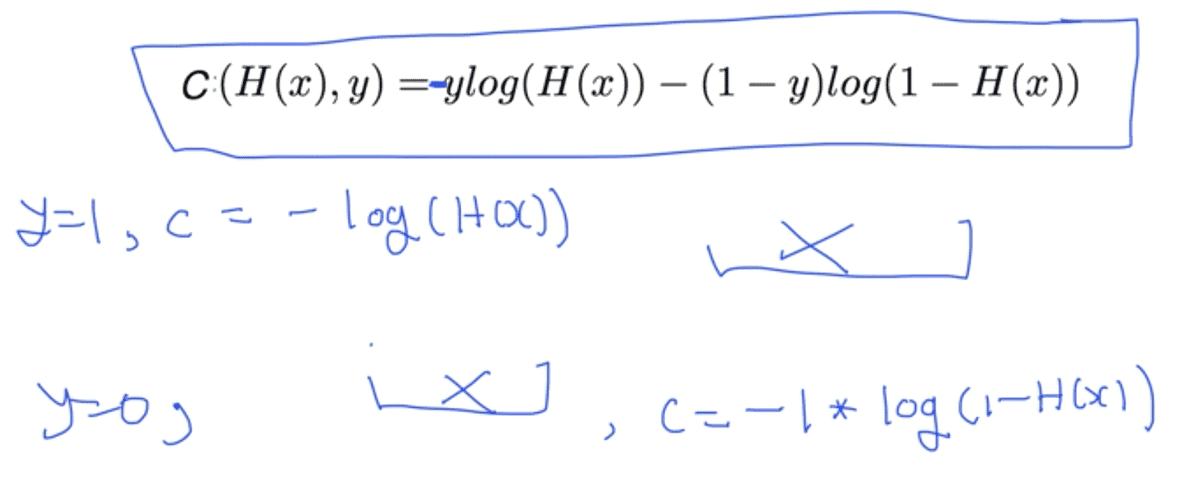
위의 유도 과정에서 조건식을 배제하고 한 줄의 수식으로 표현하면 사진과 같다. 이는 복잡해보일 수 있지만 사실 y의 값이 0 혹은 1이기 때문에 둘 중 하나를 대입하게 되면 한 개의 항은 사라지게 되고, 앞서 살펴본 조건에서와 같은 수식이 나타난다.

minimize

Gradient descent 알고리즘의 큰 틀은 Linear regression과 동일하다. 처음 Gradient를 다룰 때에는 이 알고리즘의 원리를 이해하기 위해서 미분하는 과정까지 설명했지만 사실상 이 단계 이후부터는 그러한 과정은 필요하지 않고 사진에서와 같이 Cost function만 잘 세워주고 코드를 작성할 때 제공되는 라이브러리를 잘 사용하기만 하면 된다고 한다.


5-3 TensorFlow Practice (Logistic)


recap1

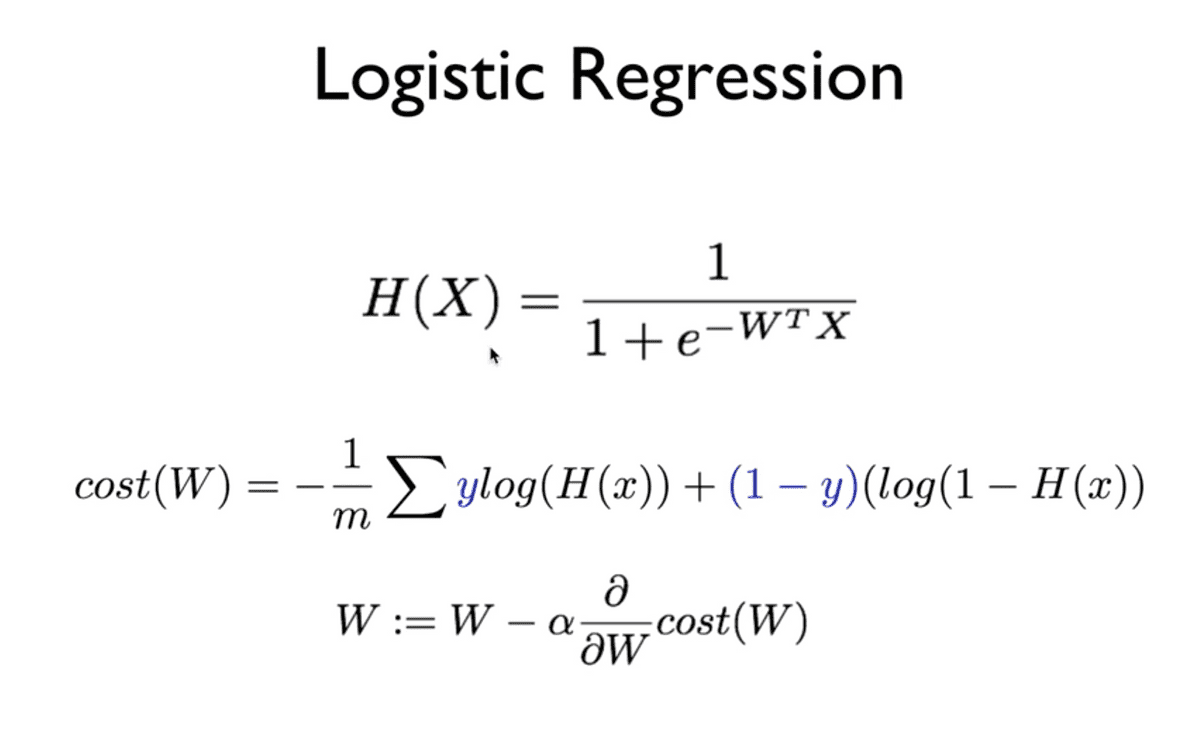
실습에 들어가기에 앞서, 우리가 이론 시간에 학습한 Hypothesis, Cost function, Gradient descent 수식은 위와 같다.

Practice 1

전체 코드를 살펴보면서 하나하나 짚어보도록 하자.

# Lab 5 Logistic Regression Classifier
import tensorflow as tf
tf.set_random_seed(777)  # for reproducibility

x_data = [[1, 2],
          [2, 3],
          [3, 1],
          [4, 3],
          [5, 3],
          [6, 2]]
y_data = [[0],
          [0],
          [0],
          [1],
          [1],
          [1]]

# placeholders for a tensor that will be always fed.
X = tf.placeholder(tf.float32, shape=[None, 2])
Y = tf.placeholder(tf.float32, shape=[None, 1])

W = tf.Variable(tf.random_normal([2, 1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')

# Hypothesis using sigmoid: tf.div(1., 1. + tf.exp(tf.matmul(X, W)))
hypothesis = tf.sigmoid(tf.matmul(X, W) + b)

# cost/loss function
cost = -tf.reduce_mean(Y * tf.log(hypothesis) + (1 - Y) *
                       tf.log(1 - hypothesis))

train = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(cost)

# 이 위까지 Graph 정의

# Accuracy computation
# True if hypothesis>0.5 else False
predicted = tf.cast(hypothesis > 0.5, dtype=tf.float32)
accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted, Y), dtype=tf.float32))

# 아랫부분은 Model을 Train하는 과정

# Launch graph
with tf.Session() as sess:
    # Initialize TensorFlow variables
    sess.run(tf.global_variables_initializer())

    for step in range(10001):
        cost_val, _ = sess.run([cost, train], feed_dict={X: x_data, Y: y_data})
        if step % 200 == 0:
            print(step, cost_val)

    # Accuracy report
    h, c, a = sess.run([hypothesis, predicted, accuracy],
                       feed_dict={X: x_data, Y: y_data})
    print("\nHypothesis: ", h, "\nCorrect (Y): ", c, "\nAccuracy: ", a)

우선 x와 y의 데이터를 명세하는 부분을 살펴보면, x는 x1, x2의 array로 구성되고 y는 0과 1, 혹은true와 false의 값을 갖게 된다. 이해를 위해 우리가 항상 예제에서 사용하던 예시를 인용하면, 어떤 학생이 x1시간만큼 x2개의 동영상 강좌를 통해 학습하였을 때, y의 결과 (pass/fail)을 갖는다고 상황을 설정해볼 수 있겠다. 또한 placeholder를 선언하면서 shape을 명세할 때, 이전 섹션에서 살펴보았던 Matrix와 관련된 개념이 포함된다.

Logistic Classification의 hypothesis는 Sigmoid function의 형태를 갖기 때문에 기존에 우리가 알고 있던 X * W + b와 같은 수식에서 끝나는 것이 아니라 TensorFlow의 내장 함수인 tf.sigmoid를 통해 쉽게 표현할 수 있다고 한다. 코드의 주석에서 확인할 수 있듯이, 수식으로 직접 표현하려면 tf에 포함된 내장 수학 함수들을 통하여 표현할 수도 있다고 한다.

또한 Cost function의 경우에는 앞서 우리가 도출한 수식을 그대로 코드로 옮겨 적으면 되고, Minimize도 GradientDescentOptimizer를 사용하여 동일하게 작성해주면 된다.

predicted는 예측한 값이 0.5(0과 1사이의 값 중 보통 기준이 되는)와 크기 비교를 하여 true와 false가 아닌 type casting을 통해 0 또는 1의 값을 갖게 된다. 그리고 accuracy는 Y값과 predicted값이 일치하는지를 마찬가지로 0과 1로 표현하여 평균을 취한 값을 갖는다.

위 코드의 실행 결과는 아래와 같다.

0 1.73078
200 0.571512
400 0.507414
600 0.471824
800 0.447585
...
9200 0.159066
9400 0.15656
9600 0.154132
9800 0.151778
10000 0.149496
Hypothesis:
[[ 0.03074029]
 [ 0.15884677]
 [ 0.30486736]
 [ 0.78138196]
 [ 0.93957496]
 [ 0.98016882]]
Correct (Y):
[[ 0.]
 [ 0.]
 [ 0.]
 [ 1.]
 [ 1.]
 [ 1.]]
Accuracy:  1.0

10000번의 반복에서 매 Step을 지날수록 Cost는 점점 매우 작은 값으로 작아짐을 알 수 있고, 학습에 의한 결과값과 예측값, 정확도까지 코드를 보면서 생각할 수 있었던 대로 결과가 도출됨을 확인할 수 있었다.

Practice 2 - Classifying diabetes

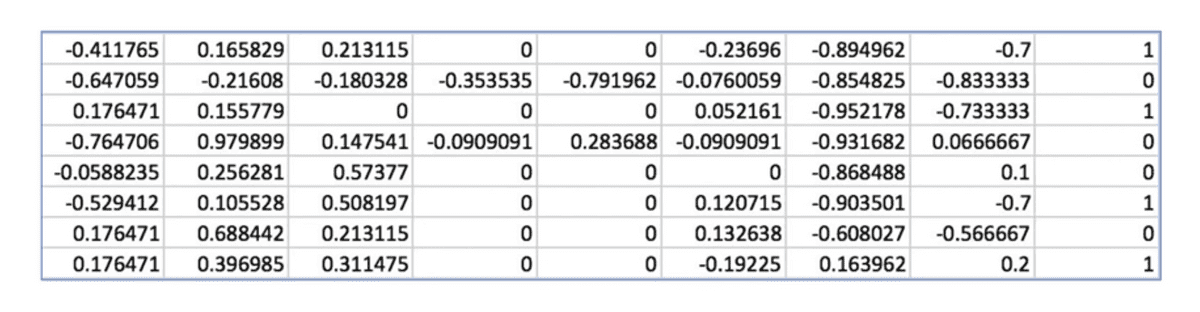
이번 실습은 주어진 혈당 수치 데이터가 있고, 이를 바탕으로 어떤 환자의 당뇨병을 예측해보는 실습이다. 이번 실습에서는 데이터가 많기 때문에 아래와 같은 데이터를 파일 형태로 저장하여 numpy의 loadtext를 매개로 사용한다.

data 

# Lab 5 Logistic Regression Classifier
import tensorflow as tf
import numpy as np
tf.set_random_seed(777)  # for reproducibility

xy = np.loadtxt('data-03-diabetes.csv', delimiter=',', dtype=np.float32)
x_data = xy[:, 0:-1]
y_data = xy[:, [-1]]

print(x_data.shape, y_data.shape)

# placeholders for a tensor that will be always fed.
X = tf.placeholder(tf.float32, shape=[None, 8])
Y = tf.placeholder(tf.float32, shape=[None, 1])

W = tf.Variable(tf.random_normal([8, 1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')

# Hypothesis using sigmoid: tf.div(1., 1. + tf.exp(-tf.matmul(X, W)))
hypothesis = tf.sigmoid(tf.matmul(X, W) + b)

# cost/loss function
cost = -tf.reduce_mean(Y * tf.log(hypothesis) + (1 - Y) *
                       tf.log(1 - hypothesis))

train = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(cost)

# Accuracy computation
# True if hypothesis>0.5 else False
predicted = tf.cast(hypothesis > 0.5, dtype=tf.float32)
accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted, Y), dtype=tf.float32))

# Launch graph
with tf.Session() as sess:
    # Initialize TensorFlow variables
    sess.run(tf.global_variables_initializer())

    for step in range(10001):
        cost_val, _ = sess.run([cost, train], feed_dict={X: x_data, Y: y_data})
        if step % 200 == 0:
            print(step, cost_val)

    # Accuracy report
    h, c, a = sess.run([hypothesis, predicted, accuracy],
                       feed_dict={X: x_data, Y: y_data})
    print("\nHypothesis: ", h, "\nCorrect (Y): ", c, "\nAccuracy: ", a)

Python List 표현식에 따라 x_data는 전체 인스턴스(:)에서 마지막 열을 제외한 모든 값(0:-1)를 저장하고, y_data는 마찬가지로 전체 인스턴스를 가져오되 마지막 열에만 해당하는 ([-1])값을 취하여 리스트로 저장한다.

shape은 데이터의 크기에 맞게 x는 8개의 변수를 가지므로 8, 결과값 y는 1개의 열을 가지므로 1을 지정해준다.

나머지의 경우 실습 1번과 마찬가지로 학습 모델을 작성해준 뒤 결과를 확인해보면 아래와 같다.

0 0.82794
200 0.755181
400 0.726355
600 0.705179
800 0.686631
...
9600 0.492056
9800 0.491396
10000 0.490767

Hypothesis:
...
[0.74610120]
[0.79919308]
[0.72995949]
[0.882917188]

Correct (Y):
...
 [ 1.]
 [ 1.]
 [ 1.]]
Accuracy:  0.762846

전체 출력이 모두 작성되어있지는 않고, 예측값은 끝부분에 해당하는 결과만을 살펴보면 학습 결과값과 예측값은 모두 정상인데, 정확도가 100%가 아닌 것을 보면 출력되지 않은 부분에서 예측이 틀린 값이 존재했던 것으로 생각해볼 수 있다.

Written by@[Anthony min]
Develop software, Develop myself, Develop life.

GitHubTwitterFacebookInstagram